prologue
Winograd是一个通过减少乘法操作来加速卷积计算的算法,在实际使用这个算法的时候,会接触到一些神奇的变换阵,这些变换阵的来历将在这一部分作为前言知识进行讲解,具体算法实现过程见mainloop部分
实质上深度学习所用的卷积是correlation(以下统一用这个词汇替代深度学习卷积)而非convolution,以下用一维序列举例,输入的两个序列长度分别为n和k,且n>k,则通常卷积(correlation)得到的结果为n−k+1,而实质上convolution得到的结果为n+k−1,这里讨论的都是步距为1的情况
convolution和correlation是两个很相似的操作:
- correlation是两个序列首元素对齐,累乘累加获取新元素,而后滑动,再计算,直至较短序列尾端碰触到较长序列尾端为止;
- convolution则是将较短序列首先进行翻转,然后尾元素对其长序列首元素,累乘累加获取新元素,而后滑动,再计算,直至较短序列头元素碰触较长序列尾元素为止.
从这个具体操作上可以证实上述关于correlation和convolution计算后的序列长度公式
实质上,convolution操作还可以表示为多项式乘法,以s(x)表示为结果项,以h(x),p(x)表示两个输入序列,convolution等价为s(x)=h(x)∗p(x),其中幂次由低到高,所对应的系数即为所求convolution结果.
而表示为多项式乘法的话,有另外一种基于多项式中国剩余定理可以构造出等价的多项式,但其乘加操作的次数是不一样的,正因如此,通过构造式构造出的s(x)存在计算更快速的可能
上述讨论的都是convolution,而实际深度学习是correlation,它俩怎么关联起来呢?实质上,这俩在构造式的结果上,只是一个转置的差别
下面基于多项式中国剩余定理,结合部分公式来说明所谓的变换阵,以及convolution和correlation的对应关系:
假设输入序列分别为[h0,⋯,hn−1]T和[p0,⋯,pk−1]T
可以用多项式对它们进行表示:h(x)=h0+h1∗x+⋯+hn−1∗xn−1和p(x)=p0+p1∗x+⋯+pk−1∗xk−1
s(x)=h(x)∗p(x)即是原先的convolution直接计算得到的结果,计算得到的最高次项为xn+k−2
基于多项式中国剩余定理可以构造出如m0(x)=x,m1(x)=x−1,m2(x)=x+1,⋯共计n+k−2项两两互质的多项式,对所有互质的多项式累乘可以得到N(x)=∏i=0n+k−3mi(x),N(x)的最高次幂是xn+k−2,与s(x)相同,可以按照多项式乘法构造出:
s(x)=hn−1∗pk−1∗N(x)+s′(x)
其中s′(x)是余项,它的次数小于N(x),这个式子可以利用定理构造出来,因为已有两两互质的多项式,而要构造s′(x)的同余方程组需先分析其对各个mi(x)取模后的情况,N(x)是mi(x)们累乘后的结果,所以该项做模运算时是0,即s′(x)=(s(x)−hn−1∗pk−1∗N(x))modmi(x)=s(x)modmi(x)=h(x)p(x)modmi(x),而这是满足模运算的分配律,故可得:
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧s0′(x)≡h0(x)p0(x)(modm0(x))s1′(x)≡h1(x)p1(x)(modm1(x))⋮sn+k−3′(x)≡hn+k−3(x)pn+k−3(x)(modmn+k−3(x))
而这其中的hi(x),pi(x)是可以计算出来的,根据h(x),p(x)去对对应的mi(x)取模,而后,基于上述信息,根据中国剩余定理可写出通式如下:
\begin{align}
s(x) &= h(x) * p(x) \,\,//\,朴素式\\
&= h_{n-1}p_{k-1}N(x) + s'(x) \,\,//\,构造式\\
&= h_{n-1}p_{k-1}N(x) + \sum_{i=0}^{n+k-3}h_i(x)p_i(x) * \frac{N(x)}{m_i(x)} * [(\frac{N(x)}{m_i(x)})^{-1}]_{m_i(x)} (mod\,\,N(x))
\end{align}
注: 该定理推导时涉及扩展欧几里得算法,裴蜀等式,乘法模逆元等知识,详见第二个参考文献的讲解
这里以F(2,3)来说明,s代表输出序列,h,p代表输入序列.其中h序列长度为2,p序列长度为3,输出序列s长度为4,同时所需的两两互质的多项式为3项,以m0(x)=x,m1(x)=x−1,m2(x)=x+1给出,同时可以写出h(x)=h0+h1x,p(x)=p0+p1x+p2x2,并且可以给出N(x)=x(x−1)(x+1)=x3−x
可以计算得到下面两个式子:
⎩⎪⎨⎪⎧h0(x)≡h0(modx)h1(x)≡h0+h1(modx−1)h2(x)≡h0−h1(modx+1)⎩⎪⎨⎪⎧p0(x)≡p0(modx)p1(x)≡p0+p1+p2(modx−1)p2(x)≡p0−p1+p2(modx+1)
由此可得s′(x)如下式:
⎩⎪⎨⎪⎧s0′(x)≡h0p0(modx)s1′(x)≡(h0+h1)(p0+p1+p2)(modx−1)s2′(x)≡(h0−h1)(p0−p1+p2)(modx+1)
同时利用扩展欧几里得算法(多项式gcd + 裴蜀等式)可求得对应的模逆元:
⎩⎪⎨⎪⎧[(x2−1)−1]x[(x2+x)−1]x−1[(x2−x)−1]x+1=−1=1/2=1/2
那么可以写出此时的convolution结果:
\begin{align}
s(x) &= h(x)p(x) = h_0p_0 + (h_0p_1 + h_1p_0)x + (h_0p_2 + h_1p_1)x^2 + h_1p_2x^3 \,\,//\,\,朴素式\\
&= s'_0(x) + (\frac{1}{2}s'_1(x)-\frac{1}{2}s'_2(x)-h_1p_2)x + (\frac{1}{2}s'_1(x)+\frac{1}{2}s'_2(x)-s'_0(x))x^2 + h_1p_2x^3 \,\,//\,\,构造式
\end{align}
实质上,像21这样啊的系数可以隐入s1′(x)里面,即可得:
⎩⎪⎨⎪⎧s0′(x)≡h0p0(modx)s1′(x)≡(h0+h1)(2p0+2p1+2p2)(modx−1)s2′(x)≡(h0−h1)(2p0−2p1+2p2)(modx+1)
其中变换阵A用于提取h序列[h0,h1]T于s(x)中的相关系数(即行数依次对应s0′(x),s1′(x),s2′(x),h1p2x3),变换阵G用于提取p序列[p0,p1,p2]T于s(x)中的相关系数(同变换阵A的对应),变换阵的行数为s(x)的项数,即n+k−1,列数为h,p序列的长度(列数对应h,p序列中的数),分别提取后可得:
A=⎣⎢⎢⎡111001−11⎦⎥⎥⎤G=⎣⎢⎢⎡121210021−210021211⎦⎥⎥⎤
B阵用于提取s(x)中各项的系数,有n+k−1项,则有对应行数和对应列数,行对应[x0,x1,x2,x3],每行中的列对应[s0′(x),s1′(x),s2′(x),h1p2]的系数,可得如下B阵:
B=⎣⎢⎢⎡10−1001100−1100−101⎦⎥⎥⎤
上述s(x)构造式的系数可以如此表示:
s=B∗[G∗p⊙A∗h]
所谓的G∗p是GEMV,⊙表示逐元素乘,实质上向量间的逐元素乘可看作对角阵乘(a⊙b=diag(a)∗b),即:s=[B∗diag(G∗p)∗A]∗h,对向量h的左侧矩阵M=[B∗diag(G∗p)∗A]做转置取逆运算,则M−1∗s=h,那么这个阵是正交阵(参考文献2评论区有人推出来的规律,利用这个规律实质上就是正交阵),根据正交阵性质有,实际可推出h=MT∗s=AT∗diag(G∗p)∗BT∗s=AT∗[(G∗p)⊙(BT∗s)] (详情见参考文献2评论区)
此刻,将s序列视为输入,h序列视为输出,p阵视为卷积核,即为1维卷积
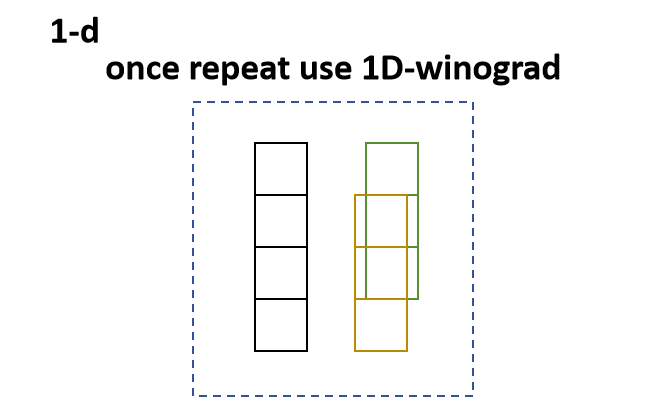
如何将1维卷积扩展到2维呢,先看下1D-winograd应用的情形,下图呈现的是F(2,3)下,长度为3的卷积核对输入序列为4进行卷积,它所呈现的重叠部分,即遇到相似的几何呈现,可以应用一次1D的winograd算法
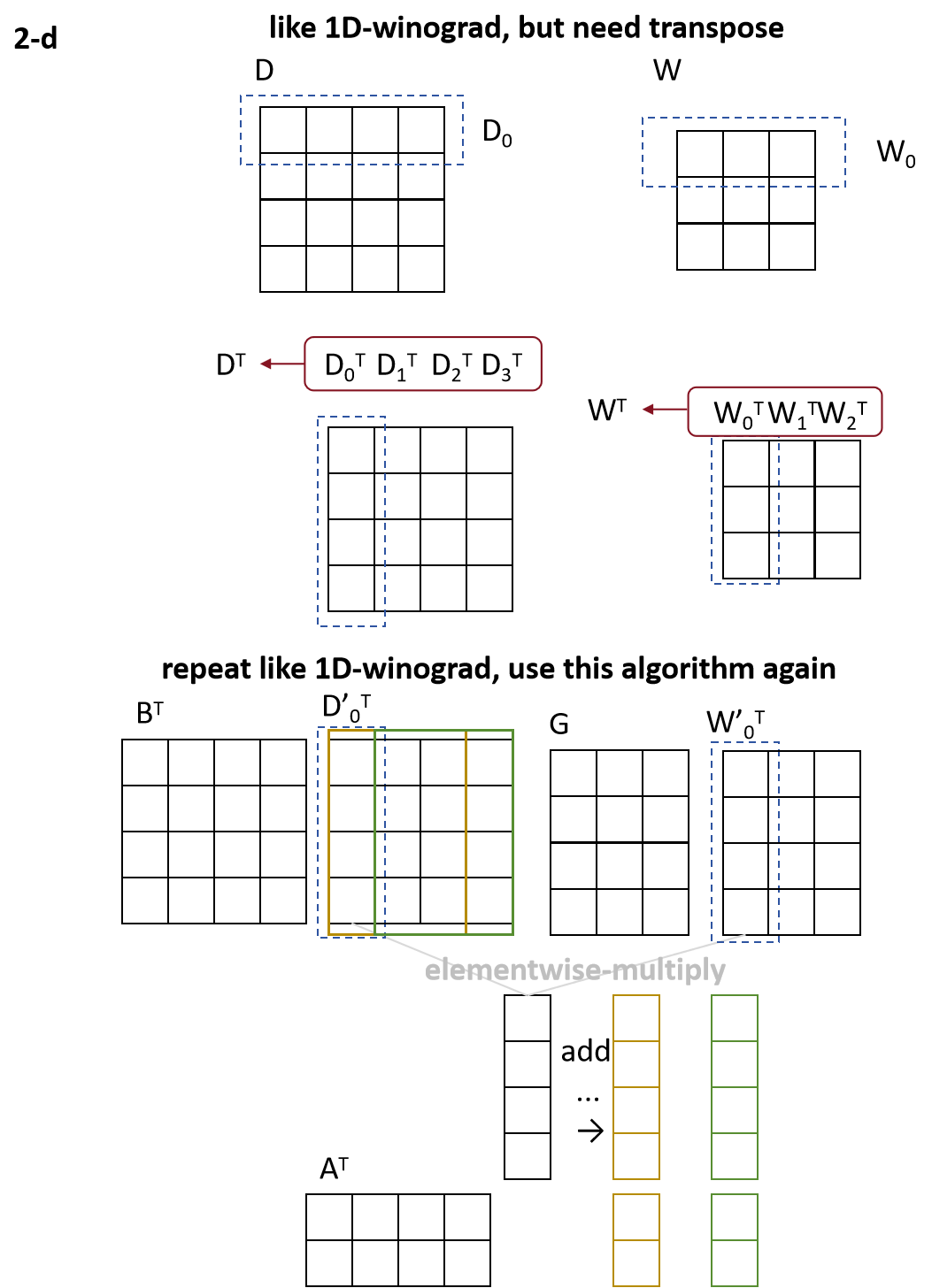
那么扩展到2D如下图所示,行方向可以应用1D-winograd算法,但需要注意,每个行向量需要转置为列向量,之余整体卷积核和输入序列,则整体各转置1次.同时后续计算可以发现,在做完1次卷积核变换和输入序列变换后,其具有高度重叠的部分,因此可再次应用1D-winograd算法,即嵌套使用2次该算法.
基于上述所说可得:
\begin{align}
Y &= A^T((GWG^T) \odot (B^TDB))A
\end{align}
实际上,我自己推的时候多了个转置😓,如下,有好心的大手子看到可以帮我看看哪里弄错了,这里的转置是基于矩阵乘加上去的(不然中间维度不等)
\begin{align}Y &= A^T[A^T[G(GW^T)^T \odot B^T(B^TD^T)^T]]^T \\ &= A^T[[(GWG^T) \odot (B^TDB)]^T]A\end{align}
mainloop
epilogue
参考文件: