flashAttention-with-cuda

从softmax变形说起

safe softmax(3-pass)

$x \in R^N$即$x$是一个长度为$N$的向量,对它进行$softmax$即有如下公式:

$$softmax(\{x_1,...,x_N\}) = \{\frac{e^{x_i}}{\sum_{j=1}^{N}{e^{x_j}}}\}^{N}_{i=1}$$

我们知道指数函数它的值随着$x$的增长是爆炸性增长的,当$x_i$大于某个值就会爆float,那么为了将它约束在fp32,即得到的值是安全的,没有上溢,可以减去一个$m(x) = max(\{x_1,...,x_N\})$,那么显然我们的$x_i-m(x)\le0$,则取到的值都是安全的.

那么整个softmax过程,可以由三个循环来表示:

• 遍历$[1,N]$,求$m(x)$,其中$m(x) = \max{\{x_i\}}$;
• 遍历$[1,N]$,求$l(x)$,其中$l(x) = \sum_{i=1}^N{e^{x_i-m(x)}}$
• 遍历$[1,N]$,求$softmax(x)$,其中$softmax(x) = [\frac{e^{x_i-m(x)}}{l(x)},...,\frac{e^{x_N-m(x)}}{l(x)}]$

online softmax(2-pass)

上面的safe softmax使用了3次循环,即需要访问gmem3次,如果可以融合中间的计算,就可以减少对gmem的访问次数,可以采用以下思路融合前两个计算:

• 遍历$[1,j]$,其中$m_{j}(x) = \max(m_{j-1}(x),x_j)$ ,其中$j\le N$;
• 遍历$[1,j]$,其中$l_j(x) = l_{j-1}(x)*e^{m_{j-1}(x) - m_j(x)} + e^{x_j - m_j(x)}$

上述式子可以进行融合,因此可以在1个循环内完成$m(x)$和$l(x)$的计算

注: 上述式子中的$l_j(x)$的计算其实把它展开来看就很好理解,因为加上一个上一轮的最大值(就是把它消掉),减去这一轮更新的最大值

上述的式子实际上就实现了分段的softmax,即softmax所要处理的一整个向量,不需要计算完全,可以逐段计算,然后利用上述思想进行合并

FlashAttentionV1

1-pass Attention

Attention计算的公式忽略对$QK^T$做scaled,以及忽略mask,可以得出简化后的Attention公式:

$$Attention = softmax(QK^{T})V$$

而MHA(Multi Head Attention)只是在这个基础上将输入的$hidden\_dimension$切成了$num\_head$份的$head\_dimension$,即内部的注意力机制的计算都是一样的,只是切成了多份进行并行计算,这里我们只考虑一个头的Attention的优化,因为别的操作一样~

其中Attention中式子产生的中间阵$S = QK^T$和$P = softmax(S)$这俩阵分别代表的是pre-softmax logits和注意力得分阵,最终期望得到的是$O = PV$.其中这里给定$Q,K,V,O \in R^{N \times d}$,$N$表示的是$sequence\_length$,$d$表示的是$head\_dimension$

根据online softmax的思路,可以描述出一个下图的2-pass的公式来计算Attention:

其中上图中的$d_i'$其实就是上述的$l_i(x)$,其中的$x_i$就是$Q$阵的第$k$行与$K^T$的第$i$行计算得到的元素,这个元素进行softmax后,作为标量$a_i$与$V$阵第$i$行进行相乘,累加到一个向量元素$o$上,最终这个值累加完后存放到结果$O$阵的第$k$行,这里需要解释的点其实就是$a_iV[i,:]$表示的含义(其实就是$P_k \in R^{1\times N}$,与$V \in R^{N \times d}$进行相乘得到的$O_k = P_kV$拆分后得到的结果),如下图所示,当i这个变量遍历完整个$sequence\_length$则底下$O^T$中的浅蓝块会变成深蓝块,即计算完毕,体现在公式则是$o_i$的更新到$o_N$:

这个2pass的Attention其实第二个循环中的值依赖于第一重循环中得到的$m_N$和$d'_N$,由此得出$a_i$,即对$x_i$做softmax后,与$V[i,:]$中对应的第i行相乘,从而更新$o_i$

如果是以$a_i$作为最后所求的值,则无法将2pass融合至1pass,但是我们所求的是$O[k,:] = o_N$,因此可以试着把中间不断迭代的$o_i$展开来看,有:

$$o_i = \sum_{j=1}^{i}{(\frac{e^{x_j-m_N}}{d'_N}V[j,:])}$$

将它分段来看,从而舍去整一行向量得到的$m_N$,$d'_N$,我们取到第i个元素的值为$m_i$,累和为$d'_i$,则原式子改写成:

$$o'_i = \sum_{j=1}^{i}{(\frac{e^{x_j-m_i}}{d'_i}V[j,:])}$$

经过裂项(裂出第i项,以寻找递推式)并整理可得:

$$o'_i = o'_{i-1}\frac{d'_{i-1}e^{m_{i-1}-m_i}}{d'_i} + \frac{e^{x_i-m_i}}{d'_i}V[i,:]$$

上面的递推式可以这么理解:将第i-1项得到的结果,将其softmax的原分母$d'_{i-1}$约去,更新内部每个元素减去的最大值,然后除于最新的累和值$d'_i$,完成前[1,i-1]的更新;并且加上此次计算得到的第i项的结果,得出[1,i]项的结果$o'_i$

根据上述递推式,可以使得Attention只需要1pass.过程如下:

Tiled Attention

这里的分块,是将QKVO进行分块,它们初始的shape都是$R^{N \times d}$,想要在1个block内的smem放下,这里假设了smem的大小是$M$,通过$B_c$,$B_r$的约束使得共享内存被最大程度的利用($/4d$是因为四个阵,它们都沿着N的方向分块,可以使得):

$K_j + V_j \lt \frac{M}{2}$

$Q_i + O_i = d * min(\frac{M}{4d},d) < \frac{M}{2}$

这样划分以尽可能多地利用共享内存

在代码实现中,由于传入的Q阵的tensor是有四个维度的数据:Tensor(b,nh,N,d)分别是batch_size,num_heads,sequence_length,head_dimension,

FlashAttentionV2

相较于V1的更新:

• 公式修改,利用Tensor Core;

  好处: 把l即softmax的分母,由12行再进行加上,这样省去了内部频繁的对l的更新

• 循环顺序调转,变成先切Q后切K,V

  好处: 原先的innerloop是切Q,即遍历$T_r$,那么每次都要load + store当前计算所需的Q,l,m,O;换了之后省去这部分频繁读写全局内存的开销,同时可以对sequence length做parallelism,这里主要体现在开grid的时候dim3 grid(Tr,b*nh),由blockIdx.y定位到负责MHA的哪一个head,blockIdx.x给你定位到这个block负责某一个head的Q的$B_r$

• 得以于上面调换顺序,使得slicedK, slicedV变成了slicedQ

好处: 这里可以从warp的内外积讨论,slicedQ只是切Q,每个Q负责到它所对应的O,他们的K,V都是一样的;而如果是slicedK,slicedV,那么一个Q它算出来每块$\hat{K}$要进行block_reduce_max,以取到当前这个块最大的m,这需要一次reduce;而后它们这些个$\hat{K_0},\hat{K_1},...$要对对应的$\hat{V_0},\hat{V_1},...$做乘积,此时是外积,做完后它们的$\hat{O}$们要做一次block_reduce_sum,可见开销很大,而slicedQ则完全不用这两次reduce

关于16816的扩展

具体实现其实也是按照公式怼,然后再优化,但是在实现的时候会发现以一个block去处理Q(Br x d) @ K^T (d x Bc)那你这个block应该分做几个warp,以4个为例,则显然你用ldmatrix去读当然是.x4最优,发射一条指令,收获个16x16大小的Q块,那么此时倒推出了Br是64,同时warp size的k跟tile size(就是block大小)的k(共有的维度的意思,mnk那个k)不一致,那就是slicedK了(这个k是head dimension),相当于外积,此时单独看一个16x16的Q块,利用16816的MMA,它对应到的K块是8x16(此时ldsm不用加.trans限定符),此时如果只与一个K块做矩阵乘,则得到的Br x Bc是64($16 \times 4$) x 8,实质上可以通过多开寄存器,多次计算实现更大的Bc

Br的维度是根据多开warp来进行扩展;Bc的维度是通过多开寄存器来扩展

因此Br,Bc的维度取决于在它们方向上的线程重复次数和寄存器重复次数,由此得到TiledMMA中的AtomLayoutMNK和ValueLayoutMNK的概念由来

网上有看到一些大佬制作类triton的DSL,其以16x16为得到的目标阵一个大小,本质上就是上面提到的repeat threads和repeat register

multi-stage

所谓multi-stage其实是结合了threadblock间并行和threadblock内并行.这里的multi所体现的是存储在smem buffer中的threadblock负责的目标块个数

得益于LDGSTS异步指令的出现,剥离了gmem到smem的约束,使得multi-stage成为可能.同时需要注意,multi-stage牺牲了部分的occupancy,以取得可能优于这部分occupancy带来的warp切换遮掩访存的优化

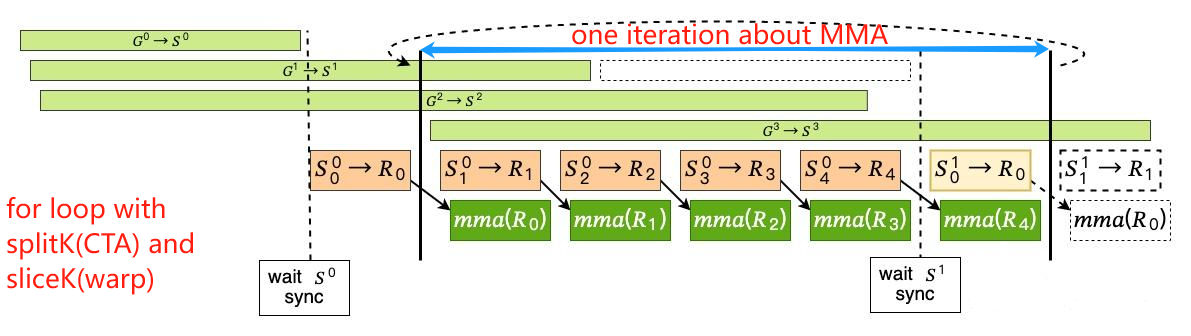
下图所体现的是一个4(k)-stage,下面简述过程(以下的tile合指同一线程块负责的A,B两个阵的目标块):

1. 利用cp.async异步拷贝k-1个tile到smem,指定对应的smem位置(单个threadblock它的smem开销大了);
2. 对应虚线前——利用cp.async.wait_group [N];去同步到指定同步点,这里的N即是k-2(允许至多k-2个没完成);
3. 对应实线前——利用LDSM完成第一个tile从smem拷贝到reg

以上是prelogue,接下来到了mainloop,mainloop这个循环对应的是splitK,即threadblock层级的K的划分:

1. 先执行第k个异步拷贝指令,提交同步点即可,无需等待;
2. 拷贝下一轮tile到reg(涉及到开多组reg,这里是2,本质上就是软流水)
3. 执行mma指令
4. 重复2,3步,这里本质上是slicedK,tile内的for loop,是warp这一层级的
5. 遇到虚线后是此次slicedK中的最后一次计算,先把下一次的异步拷贝g2s进行wait
6. 对应实线前——完成下一个tile的首个s2r,同时完成此个tile的内部的最后一次计算

重复上述步骤直至mainloop完成, 那么完成了,最终的数据都在reg,此时如果有访存密集型操作跟着的,可以合并,即算子融合,此为epilogue,那么无论你融合不融合,你数据从reg挪到gmem,要不要经过smem,视数据量而定.当然还可以开多一波寄存器,把hmma分布的数据给它搞得连续,从reg->gmem以SIMD的形式给它挪回去,当然这种做法很消耗宝贵的reg资源

FlashAttentionV3

只有阅读,没有hopper

参考文件:

• [Attention优化][2w字]🔥原理&图解: 从Online-Softmax到FlashAttention V1/V2/V3
• From Online Softmax to FlashAttention
• FlashAttention: Fast and Memory-Efficient Exact Attention with IO-Awareness
• FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning
• flash-attn-minimal
• 猛猿flashattnv1-v2